本文介绍文章 Parametrization and smooth approximation of surface triangulations 中的保形参数化算法,并给出MATLAB程序 曲面参数化问题:对于给定的三角网格曲面\(\mathbf{S}\),找到一个映射\(\phi(u,v): \mathbb{R}^2\longmapsto\mathbb{R}^3\),使得平面参数域中的点与曲面网格的点一一对应,求解参数\((u,v)\),即\(\phi^{-1}\)的过程称为参数化。
算法描述
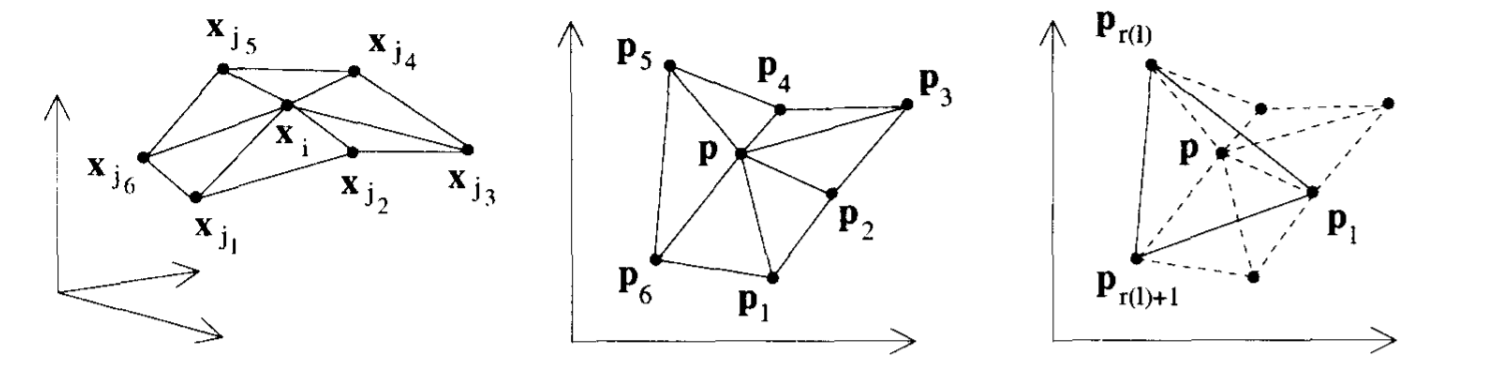
对于三角网格曲面\(\mathbf{S}\)的每个内部点\(x_i\),寻找1领域内的邻接点,将其记为\(x_{j_1},x_{j_2},\dots,x_{j_m}\),定义\(x_i\)的子图的顶点集\(X_i={x_i,x_{j_1},x_{j_2},\dots,x_{j_m}}\)表示,如上图左侧所示。
将步骤1中的\(X_i\)通过某种方式投影到平面域\(\mathbb{R}^2\)中,得到平面域中的图\(P_i={p,p_1,p_2,\dots,p_m}\)。上图中间
这里的投影方式有多种选择,文章提及到最小二乘面和平均法向面,但是当曲面中三角面片之间的夹角过大时,这两种方法不具有稳定性。于是介绍了一种W-W提出的测地极坐标映射的方法。
\[ r_k=\Vert p_k-p\Vert =\Vert x_{j_k}-x_i\Vert \]
\[ \theta_k = ang(p_k,p,p_{k+1})=2\pi \frac{ang(x_{j_k},x_i,x_{j_{k+1}})}{\sum_kang(x_{j_k},x_i,x_{k_{k+1}})} \] 这里\(ang(a,b,c)\)表示向量\(\vec {ba}\)与向量\(\vec {bc}\)之间的角度。实际上上面第二个等式就是将空间角度等比例放缩到平面中,因为平面周角为\(2\pi\),所以前面需要乘\(2\pi\)。定义\(p=(0,0)\),\(p_1=(\Vert x_{j_1}-x_i\Vert,0)\),这里\(p\)相当于极点,\(pp_1\)相当于极轴,根据极坐标\((r_k,\theta_k)\)则可计算出每个\(p_k\)。则得到平面域中的多边形\({p,p_1,p_2,\dots,p_m}\)及其内部一点\(p\)
计算\(p\)关于该平面多边形的广义重心坐标。这里采用均值重心坐标[1] 均值重心坐标的计算方式如下:
c++实现均值重心坐标可参考我的另一篇文章:均值重心坐标Mean Value Coordinates In 2D代码实现
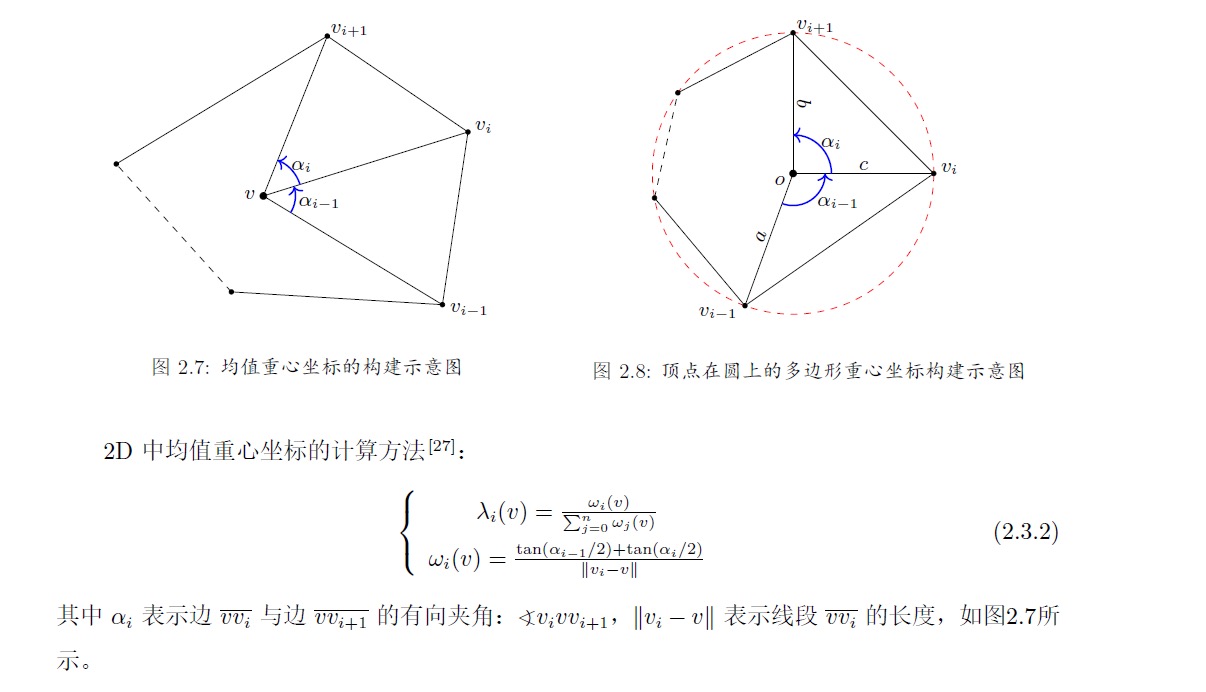
在第3步可计算出投影到平面域中的每个内部点关于1-ring点的广义重心坐标。 记:\(\lambda_i=[\dots,0,\dots,\lambda_{j_a},\dots,\lambda_{j_b},\dots,0,\dots]\),即只是\(x_i\)的邻接点对应序号中的元素为第三步计算出的重心坐标值,其余位置为0
固定边界点对应的参数(如参数化到矩形域,则将网格曲面上边界点参数有序定义为矩形域的边界) 假定后\(N\)个点为边界点,初始化\({(u_i,v_i)}_{i=n+1}^N\)
记\(\Lambda=[\lambda_1,\lambda_2,\dots,\lambda_n]^{\rm T}\),求稀疏解线性方程组:
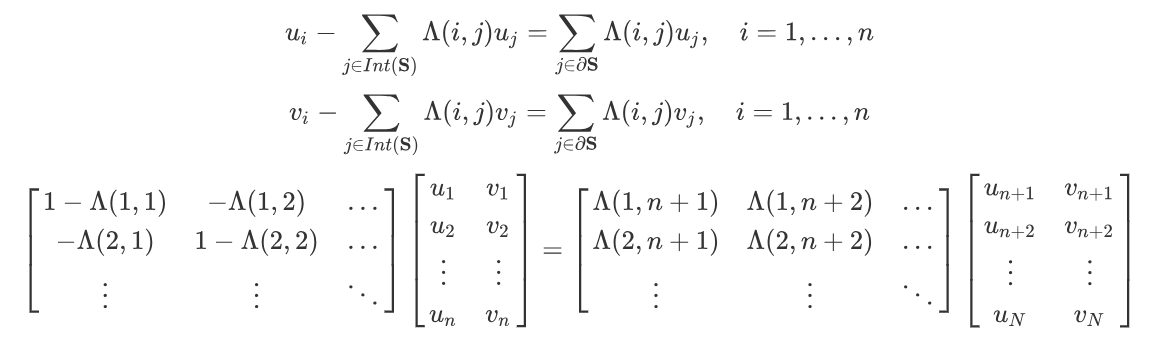
MATLAB代码
下面代码仅适用于开网格 建议在桌面端浏览器或大屏移动端查看代码
首先导入模型文件:
clear, close all model_name = 'data/bunny.obj'; [v,f]=read_mesh(model_name); % 导入模型计算边界点
boundary=compute_boundary(f); % 计算边界点,注意此时的边界是有序的 assert(~isempty(boundary),'仅适用于亏格数为0的开网格!'); MVC = sparse(length(v),length(v));对非边界点循环 计算均值重心坐标
for i = setdiff(1:length(v),boundary) % 对非边界点循环 i [~,indexes_of_adjacent_faces] = find(f==i); % 找到x_i的邻接面 adjacent_vertices = setdiff(unique(f(:,indexes_of_adjacent_faces)),i); % x_i的邻接点 %% 对空间中的x_i的无序邻接点排序 djacent_vertices_ordered = zeros(1,length(adjacent_vertices)); djacent_vertices_ordered(1) = adjacent_vertices(1); % 指定一个初始的 adjacent_faces = f(:,indexes_of_adjacent_faces); % 取出邻接面 for ii = 2:length(adjacent_vertices) [~,y] = find(adjacent_faces == djacent_vertices_ordered(ii-1)); p = setdiff(unique(adjacent_faces(:,y)),[djacent_vertices_ordered i]); djacent_vertices_ordered(ii) = p(1); end %% 投影到平面 adjacent_edges = v(:,djacent_vertices_ordered) - repmat(v(:,i),1,length(adjacent_vertices)); % X_J-X_i adjacent_edges_1 = [adjacent_edges(:,2:end) adjacent_edges(:,1)]; % X_{J+1}-X_I length_of_adjacent_edges = vecnorm(adjacent_edges,2); % 空间中邻接边的长度 cos_value = dot(adjacent_edges,adjacent_edges_1)./... length_of_adjacent_edges./[length_of_adjacent_edges(2:end) length_of_adjacent_edges(1)]; beta = acos(cos_value); % 空间中的角度beta alpha = beta/sum(beta)*(2*pi); % 计算对应的平面中的角度alpha %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % 计算平面多边形,实际上用MVC的话,就不再需要多边形的具体值了, % 因为只需要角度和长度,在上步骤已经得出 theta = alpha*triu(ones(length(alpha))-eye(length(alpha))); polygon_in_plane = length_of_adjacent_edges.*[cos(theta);sin(theta)]; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %% 广义重心坐标:均值重心坐标 tan_value = tan(alpha/2); MVC_i = ([tan_value(end) tan_value(1:end-1)]+tan_value)./... length_of_adjacent_edges; MVC(i,adjacent_vertices) = MVC_i/(sum(MVC_i)); end筛选出有用的MVC
% 只保留内部点的MVC MVC = MVC(any(MVC, 2),:);初始化边界点的\((u,v)\)参数
%% 指定边界点的(u,v) % 假定考虑参数化到[0,1]X[0,1]的正方形中 chord = vecnorm(v(:,[boundary(2:end) boundary(1)])-v(:,boundary),2); chord = chord/sum(chord)*4; uv_ = chord*triu(ones(length(chord))-eye(length(chord))); uv_1(1,:) = uv_(uv_ < 1 & uv_ >= 0); uv_1(2,:) = 0; uv_2(2,:) = uv_(uv_ < 2 & uv_ >= 1)-1; uv_2(1,:) = 1; if uv_2(2,1) < 1-uv_1(1,end) uv_2(2,1) = 0; else uv_1(1,end) = 1; end uv_3(1,:) = 3-uv_(uv_ < 3 & uv_ >= 2); uv_3(2,:) = 1; if 1-uv_3(1,1) < 1-uv_2(2,end) uv_3(1,1) = 1; else uv_2(2,end) = 1; end uv_4(2,:) = 4-uv_(uv_ <= 4 & uv_ >= 3); uv_4(1,:) = 0; if 1-uv_4(2,1) < uv_3(1,end) uv_4(2,1) = 1; else uv_3(1,end) = 0; end uv_boundary = [uv_1 uv_2 uv_3 uv_4]';构造最后一步中的稀疏线性系统
%% (I-Lambda_1)*uv_int = Lambda_2*uv_boundary Lambda_1 = MVC(:,setdiff(1:length(v),boundary)); % 构造Lambda_1 Lambda_2 = MVC(:,boundary); % 构造Lambda_2 A = eye(size(Lambda_1)) - Lambda_1; % I-Lambda_1 uv_Int = A\Lambda_2*uv_boundary; % 解线性方程组 uv(setdiff(1:length(v),boundary),:) = uv_Int; uv(boundary,:) = uv_boundary;可视化结果
%% 可视化结果 uv(:,3) = 0; plot_mesh(v,f) figure plot_mesh(uv,f)
 将绿白相见棋盘格贴图到模型表面可以直观感受参数化的好坏
将绿白相见棋盘格贴图到模型表面可以直观感受参数化的好坏 

